- lauraclark849
- Jul 11, 2025
- 39 min read
Peer Review Article | Open Access | Published 11th July 2025
Determining limit of quantification in microbiology
Jianping Jiang¹, Albert E. Parker²,³ | EJPPS | 302 (2025) |https://doi.org/10.37521/ejpps30202
Abstract
The determination of limit of quantification (LOQ) is one of the tasks specified in the validation process of a microbiological method. So far a detailed procedure for doing it is still lacking. Given the LOD (limit of detection), or data for estimating the LOD, we propose a procedure for determining the LOQ based on a Poisson confidence interval and a probability interval. This approach assures that data generated with mean at the LOQ will be higher than the LOD with high probability. We determine the required number of replicates in the validation test used to determine the LOD and the LOQ using the negative binomial probability density function that models over-dispersion of growth media plate count data in validation tests. The objective is to facilitate the determinations of some parameters commonly used in microbiological testing, such as setting control limits and suitable number of growth media plate counts.
Key words: microbiological methods, limit of detection (LOD), limit of quantification (LOQ), confidence intervals.
INTRODUCTION
The traditional method for quantifying microbial abundances in microbiological testing has been growth media cultivation and counting individual microbes. In the growth media method, a liquid bacterial sample is placed onto an agar plate containing a suitable growth medium. After a period of incubation, bacterial cells form colonies visible to human eyes. These colonies are counted and the bacterial concentration in the original suspension is estimated.
In recent years new technologies have emerged in the field of microbiological testing. Instead of growth media incubation, these new technologies use alternative methods, such as chemical reagents or optical detection, to detect and quantify the bacterial cells in a sample. These new microbiological methods (also termed “alternative microbiological methods”) usually have the advantage of faster detection time and higher sensitivity than traditional growth media based methods.
To ensure the validity and usefulness of the new microbiological methods, governmental regulatory agencies, e.g. European Pharmacopoeia (E.P. 5.1.6)¹ US Pharmacopeia (USP<1223>)², and industrial groups, e.g. Parenteral Drug Association (PDA Technical Report TR33)³, request validation tests and have provided guidelines for validating alternative microbiological methods.
Two quantities estimated from these validation tests are the limit of detection (LOD) and the limit of quantification (LOQ). Regulatory and industrial guidelines are vague regarding how to determine either the LOD or LOQ. For example, USP<1223>² and PDA Technical report TR33³ define the LOD as “The lowest concentration of microorganisms in a test sample that can be detected” without specifying any measure of statistical confidence or power. However, recent literature of Sharp et al.⁴ applies the ideas promoted by Currie⁵ to determine the LOD for microbiological assays with a specified level of statistical power as part of the validation process. The guidelines and literature are even less instructive in the determination of LOQ. For example, USP<1223>² and PDA Technical report³ define the LOQ as "The lowest number of microorganisms in a test sample that can be enumerated with acceptable accuracy and precision" without specifying any measure of statistical confidence or power.
Due to the high variability of the distribution of environmental microbes in the environment, there are considerable difficulties in the determinations of some environmental monitoring parameters, such as setting of control levels in cleanrooms, Whyte 2020⁶, and the suitable number of colonies in growth media plates, Tomasiewicz 1980⁷. We submit that a statistical approach to LOD and LOQ might facilitate in practical determinations of those microbiological parameters.
This paper offers a proposal to determine the LOQ in microbiological method validation after the LOD has already been calculated theoretically (e,g., the LOD approaches due to Kaiser 1965⁸ Sharp et al 2023⁴) or after the LOD has been determined experimentally.
Background on LOD and LOQ from Chemistry
Limit of detection and limit of quantification are familiar concepts in analytical chemistry and instrument engineering. Large volumes of literature can be found expounding these concepts.
Beyond the arithmetic elaborations, the essential components of the process of determining LOD based on blanks in chemical analysis are clear. This process involves both experimental and statistical tasks. A brief description of the process of LOD determination in analytical chemistry that attains a specified level of statistical confidence given data from blanks is as follows.
Step 1- Collect blank measurement data: prepare samples of blanks, which do not contain the targeted chemical (analyte). Use an analytical instrument to measure these blank samples, record the instrument readings (voltage, current, or other engineering parameters), calculate the mean value (xᵇˡᵃⁿᵏ) and standard deviation

of these blank sample measurements.
Step 2 - Estimate the LOD from the blanks. According to Kaiser 1973⁹, LOD is the lowest concentration in a sample which can be distinguished from blanks by the analytical instrument with high probability (see also Keith 1983¹⁰, Currie 1996⁵). The requirement for quantitative LOD metric of this instrumental capability is as follows,

The multiplier k is sometimes set to 3 (Keith et al 1983¹⁰) or sometimes to 3.3 (CLSI 2004¹¹).
Step 3 - Collect LOD measurement data: prepare samples of LOD test, which contain low concentration of the analyte. The suitable LOD samples are usually prepared by serial dilutions of the target analyte to obtain a range of low concentration (c) solutions. Use the analytical instrument to measure these LOD samples, record the instrument readings (voltage, current, or other engineering parameters), and from the n LOD sample measurements at each concentration (c) calculate the mean value (xLOD(c)) and standard deviation (sLOD(c)) . The LOD is the concentration of analyte c*, at which the analytical instrument is capable of producing a signal xLOD estimated in equation¹,

The relationship between measurement signal strengths of an instrument and LOD value is illustrated in Fig. 1 (Kaiser 1973).

The statistical interpretation of eq.(1) is as follows. An analytical instrument will have an uncertainty in its measurement of a sample. The solid black curves in Fig. 1 represent the fluctuations of the signals from the instrument. These fluctuations are caused by instrument errors, uncertainty in sample preparation as well as random noise during the measurement process. As an engineering requirement, the signal strength of the instrument in LOD sample measurement (Fig. 1(B)) needs to be higher than that of blank sample measurement (Fig. 1(A)). Because of the measurement fluctuations, there is uncertainty in determining the signal xLOD and xLOD(c*) in LOD measurement, as shown in the shaded area in Fig. 1, which is termed the “perturbation zone” by Kaiser (Kaiser 1973⁹). Kaiser’s treatment of LOD determination was from an engineering instrumentation aspect of analytical chemistry. He emphasized the necessity of taking measurement uncertainty into consideration in obtaining a numerical value of LOD, which brought clarity into the practical process of obtaining LOD from blank samples. Kaiser’s “perturbation zone” denotes the rough extent of the analytical measurement uncertainty (both in analyte sample preparation technique and in analytical instrument accuracy). However, Kaiser was not explicit in defining the “perturbation zone” in standard terminology of mathematical statistics. It will be helpful for practitioners to interpret Kaiser’s treatment of LOD in terms of statistics. In an analytical chemical measurement, the actual concentration of an analyte in a solution is a fixed but unknown numerical parameter. Due to random errors in experiments, any measurement of a concentration will be an approximate estimate. In terms of statistical theory, confidence interval (CI) is often used to denote a range of estimates for an unknown parameter. Limit of detection (LOD) is simply the lowest level of analyte concentration, at which a specific instrument can measure with a tolerable amount of error. In LOD measurement, a practical question could be as follows: “how certain can I be that I am measuring the real concentration of the target analyte rather than the random fluctuation of a blank sample?” In this case, a CI can be used to provide a range of estimates for the true value of LOD at a given level of confidence given the n LOD samples with mean xLOD(c*) and SD sLOD(c*). Practically speaking, the higher the assigned value of LOD, the higher the confidence level that that LOD value is away from an erroneous reading of a blank sample. Therefore, a confidence level is useful for designating how high a mean signal from LOD samples (xLOD) should be above that of mean of the blank samples (xblank). In case of

from equation (1), there is at least 98.5% confidence level that LOD is higher than true mean blank signal, assuming a normal distribution of instrument measurements of at least n=3 blank samples (see Appendix 3).
The limit of quantification (LOQ) is a concentration of analyte, above which the quantitative measurement is possible. There is no regulatory or standard guideline for assigning a numerical value for LOQ. The industrial convention of LOQ definition in analytical chemistry is as follows (CLSI 2004¹¹, Keith et al 1983¹⁰),

where xLOQ is the instrument reading of samples prepared for LOQ test.
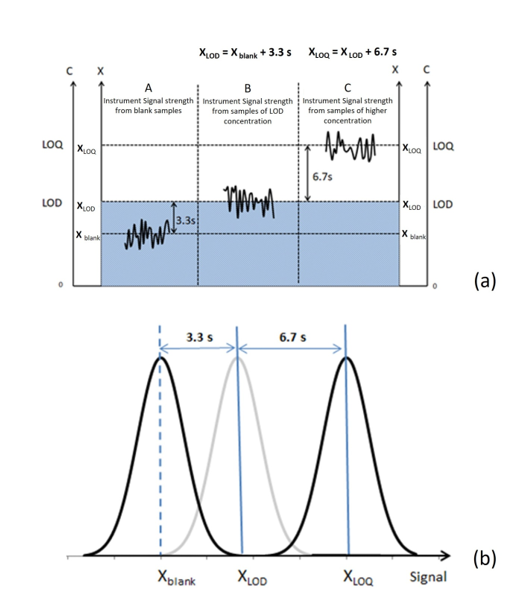
As shown in Fig.2 (a), if the concentration of analyte in a sample is high enough so that the instrument reading xLOQ is sufficiently higher than the shaded “perturbation zone”, then there will be assurance that the influence of random fluctuation is negligible and quantitative measurement is possible. As in the case of LOD measurement, the practical question is “how assured can I be that the proposed value of LOQ is high enough above random fluctuation to allow quantitative measurement?” Again, a confidence level of such an assurance is desirable for providing guidance to the experimenters. With the definition of LOQ as in eq. (2), at a 99.6% confidence level, the LOQ is above the “perturbation zone” (Appendix 3) (i.e., above the true mean LOD signal) as shown in Column C in Fig. 2(a), with normal distribution assumption of the measurements collected from at least n=3 LOD samples¹¹. Perhaps more importantly, we can make a probability statement about data that may be generated at the LOQ. With the definition of LOQ as in eq. (2), with at least 90% confidence, 90% of the data generated at the true mean LOQ signal is above the “perturbation zone” (Appendix 3) as shown in Column C in Fig. 2(a), with normal distribution assumption of the measurements collected from n=4 LOD samples¹¹. If there are n=6 LOD samples, with at least 95% confidence, 90% of the data generated at the true mean LOQ signal will be above the true LOD.
Keith et al 1983¹⁰ gave the statistical interpretation of signal strength of blank, LOD and LOQ in terms of the normal distribution curve assuming equal variances, although, unlike the previous example, they assumed that the variance was known. This interpretation is reproduced in Fig. 2(b). The background noise and instrumental error dominate in Kaiser’s perturbation zone of ± 3.3s around xblank, termed “region of high uncertainty” by Keith et al¹⁰. The LOD denotes the upper boundary of this high measurement uncertainty region. In order for quantitative measurement to be practical, the measurement uncertainty will need to be significantly lower, away from the “region of high uncertainty”. As shown in Fig. 2(b), if a measurement is made at a concentration level producing a signal strength xLOQ, which is 6.7s higher than xLOD, there will be a very high probability (about 99.8% when the data are as shown in Figure 2) that this signal is different from those produced by n≥3 blank samples. Therefore, the value of xLOQ marks the starting point of the “region of quantification” in Keith et al 1983¹⁰.
Another representation of the relationship between LOD, LOQ and instrument signal strengths (x) is shown in Fig.3 below. Some salient points are illustrated in this graph: (a) blanks, LOD and LOQ are expressed in terms of reagent preparation, in the units of per volume or per weight. Their uncertainties are determined by metrology in chemistry and are empirically known quantities before a test; (b) xblank, xLOD, and xLOQ are engineering parameters of an analytical instrument, expressed in the units of mV, mA or other engineering units. Their uncertainties (expressed as standard deviations s) are unknown a priori and need to be determined through tests; (c) the shaded area in Fig. 3 represents the area where the noise and errors have significant influence in analytical instrument measurement. This is the “perturbation zone” of Kaiser 1973⁹ and “region of high uncertainty” of Keith et al¹⁰.

Background on LOD and LOQ in microbiology
For microbiological data, the conceptual definitions of blank, LOD, and LOQ determinations can be similar to those in analytical chemistry. One crucial difference is that blanks can be very challenging if not impossible to generate in microbiological testing. Another crucial difference is that microbiological data are often in the form of discrete counts, such as colony-forming-units (CFU); while the analytical chemical tests yield measurement data in continuous numerical values, such as electrical voltage. Hence, from the statistical point of view, the data analyses are necessarily different for analytical chemical samples and for microbiological ones. In low concentration measurements of microbiological samples, the discrete count data values are usually quite low, for which normal distribution calculations are not applicable. Instead, specialized statistical distributions, such as Poisson and negative binomial, are needed. We also consider results from assays that only determine the presence or absence of microbes. In the next sections, the methods of determining LOD for these different types of microbiological data will be reviewed.
For a new microbiological technology, the instrument is an analytical device which measures some aspects of chemical or physical characteristics of a bacterial cell. As an example, in an ATP (Adenosine triphosphate) based microbial sensor, the fluorescence emission by bacterial cells is measured and correlated to the bacterial load in a sample. This type of technology usually is a qualitative detection method, which provides a presence/absence classification of a sample. Another example of a new microbiological method is the fluorescent microbial counting device, such as BioTrak of TSI, RMS of Mettler Toledo and BAMS of MicronView. In these devices, the fluorescence emission of a single bacterial cell is detected and used as a bio-marker to differentiate microbial cells from inert particles. The readings of these fluorescent particle counting devices are counts¹². These types of new technologies that generate counts are the focus of this article.
In terms of test data analysis, both traditional growth media plate count methods and the new methods using fluorescent particle counting technique yield discrete values in their data output. Therefore, the data from these two types of methods can be analyzed by the same sets of statistical tools. They also face similar technical challenges in determining LOD and LOQ.
Regulatory agencies and industrial standard organizations require that new microbiological methods be validated to demonstrate their efficacy for the measurement of microbes. In a validation test of a new microbiological method, a traditional growth media plate count method (compendial method) is used as reference, to which the new method will be compared. LOD and LOQ determinations are part of the acceptance criteria in the validation protocol.
The determination of LOD of a microbiological method is of the same concept as that of analytical chemistry. However, unlike chemistry, the “blank” sample is not easily obtainable in practical microbiology tests. This is a crucial difference between LOD determinations in microbiology and in analytical chemistry. So instead of defining the LOD and LOQ with respect to blank samples as in equation 1 and equation 2, they are determined experimentally by using low concentrations of the microbes over many dilutions as described below. The special challenge for LOD in a microbiology method is the difficulty in preparing and measuring these low concentration titers of the bacterial suspension. This difficulty is due to both the potentially heterogeneous distribution of the bacterial cells in a liquid solution and the fickleness of living bacterial cells under cultivation.
Regulatory agencies and trade organizations have given specific guidelines for the process of obtaining LOD in a validation test. USP<1223> provides 2 options for determination of LOD². Option 1 is the approach to use when the response is a count. Option 2 is when the response is presence/absence.
Option 1: “Inoculate a suitable diluent solution with a serial dilution range of each challenge microorganism, appropriate for the intended use of the method and the technology. In most cases, the compendial media growth promotion test panel may be sufficient. The level of inoculation should be adjusted to a target of 50% of the dilution samples that show growth in the compendial test.”
Option 2 (MPN—Most Probable Number method): “Create a dilution series of the challenge organisms in a suitable diluent solution to include at least the range of 10¹ cfu to 10⁻² cfu (for a 10-fold series) or 5 cfu to 10⁻¹ cfu/inocula volume (for a 2-fold dilution series). Perform both the compendial and alternate tests with at least 5 simultaneous replicates of each dilution from the chosen series. Determine the most probable number (MPN) from three dilutions in series that provide both positive and negative growth (or signal).”
In both options, the result of the comparison test of new method versus compendial method is to be evaluated to establish the ability of the 2 methods to detect the presence of low numbers of microbes in test samples. Once the similarity of this ability of new method to compendial method is established, the LOD of the new method is deemed to be the bacterial concentration of the LOD titer as measured by the compendial method.
By following either Option 1 or 2, there will be a high probability that the test samples contain sufficiently low concentration of microbes for a valid LOD determination. In either of these two options, the theoretical value of LOD is the lowest concentration of microbes in test samples that have a 95% chance (or power) of being detected (Currie 1996⁵, Sharp et al 2023⁴). In other words, in the current practice of microbiological testing, LOD is not determined by studying “blank” samples. This is a different approach to determining the LOD compared to what we explain above for chemistry which is based on assessing blank samples. This is because in many instances blank samples are not possible to generate, e.g. for very sensitive clean room microbe detectors, there will always be some microbial contamination. On the other hand, when assessing CFUs in lab systems with a well-defined inoculum of a target species (e.g., biofilm tests of Pseudomonas aeruginosa), it is perfectly feasible to generate blank samples with no target microbes, in which case equations¹ and² would result in the estimates LOD=LOQ=0 because the mean and SD of the blanks would be 0. Nonetheless, there are certainly microbiological systems that do generate a non-zero mean and SD when analyzing blanks with no microbes, e.g., a fluorescence technology may incorrectly identify abiotic particles in a blank sample as microbes. Below (e.g., in Fig 4 and 5), we still consider “hypothetical blank” samples for illustrative purposes as a useful teaching tool to bridge to analogous concepts in analytical chemistry.

In microbiological tests, especially at low microbial concentration, the microbial count data exhibit random fluctuation around an average count value. This random fluctuation is commonly modeled by a Poisson or negative binomial distribution. Analogous to the blank sample in analytical chemistry test, a hypothetical blank sample in a microbiological test is the one that contains no microbes and hence would never show microbial growth on a growth medium plate. On the other hand, due to the random distribution of microbes in a sample, zero growth on a medium plate does not necessarily mean that there is zero microbes in the sample. When a random plate count yields a zero, there’s a probability that the microbial sample actually contains a low concentration of microbes but they were missed in the collection process. From Poisson distribution calculation, at 95% confidence, the true number of microbes per plate is as high as 3 when a plate count of 0 is observed (i.e., when Poisson variable x=0).
As explained above however, the LOD in microbiology is not based on blank samples with no microbes. Instead, the LOD is either based on data or the result of a theoretical calculation that gives the lowest number of microbes that can be detected with high statistical power. As an example of the latter approach, again consider a Poisson random count, for which probabilities are calculated by

When the true number of microbes is λ = 3/plate, then the Poisson model predicts that the probability of observing a zero plate count is P(0, 3) ≈ 0.05, which indicates a false negative rate β = 0.05. Or equivalently, there’s 95% power to detect at least one microbe in a plate volume when there truly are LOD = 3 microbes per plate volume. Viewing this statistical concept from practical microbiology laboratory practice angle, this example shows that even if, by sufficient test procedure, one establishes that a microbial sample contains an average value of 3 microbes (i.e. λ = 3/plate) in a given volume, there still is a small probability (β = 0.05) of that sample volume yielding zero CFU (x=0) in any single random test. This demonstrates the complexity of microbiological testing and it calls for careful statistical treatment of plate count data. In microbiological tests of low concentration samples, such as the method validation test for LOD determination in Options 1 and 2 above, it is prudent to be mindful of the false negative rate when taking sample measurements. A multiplicity of replicates in sampling is often necessary to keep the false negative rate (β) and power (1-β) at acceptable levels, e.g., a false negative rate β = 0.05 and power of 0.95. The idea of this paper is to apply this approach to define the LOQ as the mean value such that data generated around that mean value have a high probability of being above the LOD. In this example, when LOD=3, then when Poisson data are generated around mean LOQ=7.8, there is a 95% chance that the Poisson data are above the fixed value of LOD=3 that was calculated using theoretical calculations.
Figure 4 is a graphic illustration of the uncertainty in microbial count data generated from hypothetical blank data and from data with mean at the LOD. The LOD data are generated at low concentration measurements in a comparison test between a compendial method and a new microbiological method. In this graph, the count data from compendial method is marked X, and those from the new method is marked Y. The 95% confidence interval of a Poisson rate generated from data from blanks is denoted by the axis marked CI. Figure 4(A) shows that the 95% confidence interval of blank sample measurement is from 0 and 4, marked by the shaded area. In the measurement of the LOD titer, per regulatory guidelines (PDA 2013³, USP 2015 ²) there are roughly 50% of samples showed microbial growth as shown in Fig. 4(B). According to the guideline of USP<1223> (Option 1 above), from a test data set of multiple microbial samples the value of LOD can be obtained by calculating the average microbial count from the replicate samples and then dividing the average count by the volume of the sample collection, i.e.

In statistical terms, the average microbial count is the maximum likelihood estimate of Poisson parameter λ, which is the true microbial distribution in the test sample. Assuming 8 replicates with 4 showing growth (with 1 CFU in each replicate) and 4 of them showing no growth, then the true microbial density in the sample is estimated by LOD= (4x1 + 4X0)/8 = (4 CFU)/(8 plates).
The shaded area in column B of Figure 4 represents the 95% confidence interval for the true LOD [1, 10] CFU across 0.8ml in 8 plates - see Appendix 1. As we saw before for chemical assays, this CI is the “perturbation zone” of Kaiser⁹ and “region of high uncertainty” of Keith et al¹⁰. Using the idea in this paper, we will set the LOQ=(17 CFU)/(8 plates) so that data generated with mean equal to the LOQ will have probability 0.95² = 0.90 of being above the LOD. The LOD and LOQ can be scaled to physically units. When the volume plated is 0.1ml, LOD=4 CFU/(8 plates) = 0.5CFU/plate = 5CFU/ml (with 95% CI [1.25, 12.50] CFU/ml); LOQ = (17 CFU)/(8 plates) = 2.1 CFU/plate = 21 CFU/ml.
Several researches have pointed out the fact that plate count data in microbiological tests exhibit over-dispersion, that is, the variance of the plate count data is larger than that given by a Poisson distribution model (Sharp et al 2023⁴). As a result of this extra-Poisson variability, an estimate of LOD by Poisson model may be overly optimistic. These researchers proposed an improved model using negative binomial distribution function to account for the over-dispersion when estimating LOD of microbiological tests. In addition, Sharp et al⁴ showed how the LOD depends on the number of replicates (n) of microbiological samples. Consequently, the negative binomial LOD model provides a valuable tool in determining the requirement of the number of replicates (n) in a microbiological test for a desired false negative rate, for example, β=0.05.
One common operational practice in a microbiological test is to define the plate count of 1 in a poured sample on a growth medium plate as the limit of detection, i.e. LOD = 1 CFU per poured volume of the sample (Sutton 2011¹³, PDA 2013³). For a single sample (replicate number n=1), it has been shown that both Poisson and negative binomial models indicate that if there is 1 CFU/plate in a volume, then the false negative rate β>0.36. That is, with probability 0.64, 1 CFU will be present in a plate volume. However, if multiple replicates of plating (n>1) are taken for the same sample, the false negative rate will be reduced steadily as the number of replicates n increases (Sharp et al 2023⁴). That is, with probability 1-β, at least one of the n replicates will yield some CFUs. It is then apparent that with a sufficiently large number of replicates (n) in a microbiological test, 1 CFU/plate in a sample can be detected with a satisfactory false negative rate, e.g. β = 0.05. In this paper, we strive to work out the requirement for the number of replicates (n) to achieve such a goal. Since the negative binomial model gives a more stringent value of the minimum detectable number of CFU than the Poisson model, we will use negative binomial probability density function to determine the required number of replicates n in a microbiological test so that as few as 1 CFU/plate can be detected with high probability, say 1-β=0.95. The resultant requirements for the number of replicates are shown in Table 1. As expected, the data set with higher variability (larger coefficient of variation CV) will need a larger number of replicates (n) to fulfil the statistical requirements.

In various regulatory guidelines for validation of microbiological methods, the number of replicates in test samples is specified. For example, USP<1223>² recommends that “the limit of detection of an assay is determined from a number of replicates (not less than 5).” The formulation of the number of replicates by negative binominal model, as seen in Table 1, provides ample justification for this recommendation by USP<1223>. With number of replicates n>5, the false negative rate β will be contained within a reasonable range, even for quite severe extra-Poisson variability (e.g. CV=1). PDA guideline for number of replicates (n) for LOD determination is more stringent. In PDA TR33³, it recommends that for limit of detection test “to use not less than 10 replicates per dilution”, which provides assurance of low false negative rate for even larger variability in plate count data.
The work of Sharp et al⁴ showed that assuming Poisson variability in a low concentration sample could lead to underestimate of false negative rate when there is extra-Poisson variability. This emphasizes the importance of sufficient number of replicates in LOD tests. Since the coefficient of variation (CV) is not known a priori, in a test to determine LOD, it will be prudent for the experimenters to follow closely the requirement of replicates recommended by regulatory guidelines for the sake of adequate false negative rate.
A new approach for the LOQ in Microbiology
In the previous section we showcased how to calculate the LOQ given either theoretical value of the LOD or given data generated at the LOD as per PDA and USP guidance documents. Here we formalize the calculation of the LOQ.
Regulatory agencies and trade organizations only provide broad stroke guidelines for the determination of LOQ in a microbiological method. PDA Technical Report TR33 provides: “To demonstrate this, confidence intervals of count results assuming a Poisson distribution may be used. To that end, Poisson confidence intervals for the count results of the existing method may be calculated.”³
As we showed earlier, in analytical chemistry tests, there’s a distinction between the determination of limit of detection (LOD) and that of limit of quantification (LOQ): namely, the process of determining LOD is essentially an engineering procedure of generating experimental data and doing statistical data analysis, while the determination of LOQ is purely a task of statistical analysis. For a test result to be quantitative, it needs to have assurance that the influence of noise is at a sufficiently low level. Kaiser’s “perturbation zone” concept is a graphic illustration of the extent of the zone of noise influence. In other words, the level of LOQ is so determined that the signal strength from the chemical analyte is far enough above the “perturbation zone” to ensure that a quantitative measurement can be made. It will be helpful to give Kaiser’s concept of “perturbation zone” a statistical meaning. For analytical chemistry tests, we propose to treat the extent of this “perturbation zone” as the confidence interval of the measured signal of “blank” sample (at a given level of confidence). Consequently, the LOQ of a chemical test can be viewed as a value such that data generated at that value do not overlap with the “perturbation zone” at an acceptable level of confidence. As in analytical chemistry, the process of determining LOQ in a microbiological method is essentially a task in statistical analysis. One difficulty arises in microbiological tests because of the lack of “blank” sample of a microbiological nature. To circumvent this difficulty, in this article we propose to use the value of LOD obtained in a microbiological test as baseline for the task of determining LOQ by statistical analysis. Consequently, the prerequisite of this LOQ determination process is the successful experimental determinations for LOD and linearity of a new microbiological method in a comparison test against a compendial method. Per industrial guideline, statistical tools for Poisson variable are to be used for this process.
The limit of quantification (LOQ) is commonly defined in analytical chemistry as “the lowest concentration of measurand that can be determined with an acceptable level of repeatability, precision and trueness”¹⁴. The same concept is applicable also in microbiology. The task here is to define an acceptable level of repeatability for microbiological count data. As in analytical chemistry, the concept of confidence and probability intervals can be used in microbiological tests to provide a metric for determination of an acceptable level of repeatability.
The purpose of this note is to propose a scheme based on Poisson confidence and probability intervals to determine the limit of quantification (LOQ) for microbiology methods. The goal is to provide an LOQ for which Poisson count data generated with mean at the LOQ is distinguishable from that of LOD at a high confidence level.

In this proposal, confidence and probability intervals based on Poisson variables will be used for determining the LOQ of a microbiological method. The determination is done in a stepwise process. The first step is to obtain by experimental test and statistical analysis the limit of detection (LOD) of the microbiological method, as described in the previous section. The next step is to determine the upper limit of the confidence interval of the true value of LOD. This can be done by numerical calculation or consulting a Poisson confidence interval table at a suitable level of confidence. In Appendix 1 of this note, such a table is provided. For illustration purpose, let’s discuss a hypothetical microbiological test, in which a limit of detection (LOD) had already been estimated as LOD=4CFU/(all replicate samples) in a laboratory test following USP<1223> guideline. Figure 5 gives a graphic illustration of the confidence interval at 95% level for the measured value of the LOD titer sample. In this case, the upper limit of confidence interval is approximately 10. The objective in assigning a value to LOQ is that data generated with a mean at this value at the LOQ is distinguishable with high confidence from the true value of LOD. In terms of statistical analysis, such an objective can be achieved by selecting the LOQ so that counts generated with a mean at the LOQ have a high probability of being greater than the upper confidence limit of the value of LOD. If LOQ is assigned as 17, data with mean at LOQ have a 95% chance of being larger than 10, which is the upper confidence limit of LOD = 4 and so there is 0.952 = 0.9 probability of being larger than the true LOD. Figure 6 shows probability functions with the expected values of LOD=4 and LOQ=17 and the relative positions of upper confidence limit for the LOD and the lower probability limit for the LOQ.

In summary, the proposed process of determining LOQ of a microbiological method is as follows:
Step 1: determine experimentally the limit of detection (LOD) of the microbiological method, following regulatory guidelines and use of appropriate statistical tools, such as the requirement for sufficient number of replicates in the LOD titer testing to ensure adequate false negative rate.
Step 2: Using the data from Step 1, use the sum of Poisson counts over all samples to calculate the 95% upper confidence limit of the true LOD value.
Step 3: by calculation or by consulting a statistical table, find an LOQ such that the sum of the Poisson data generated at the LOQ has a 95% chance of being higher than the UCL from Step 2. The formula to scale the LOQ to physical units is as follows,

For reader’s convenience, the next section shows how to calculate the LOQ and Appendix 2 provides look-up tables for the LOQ at confidence levels of 95% and 99% respectively.
Numerical calculation of Poisson confidence intervals
The remaining technical task is to find a suitable method for obtaining the numerical values of confidence intervals of Poisson expected value and probability intervals for the LOQ at various percentage levels. This Poisson approach is applicable when a growth medium plate count method, such as “Option 1” in USP<1223> guideline mentioned in the previous section, is used.
As described in previous section, in the formulations of LOD and LOQ in analytical chemistry the parameters for normal distribution are used. Normal distribution is a commonly used statistical model and convenient to use. However, for small expected values of microbial count data, normal distribution is not a suitable model for data analysis. In microbiological tests for determining LOD and LOQ, the concentration of microbes in a sample is low, therefore, the number of detected microbes is small. To describe this sort of occurrence where the number of events is small, Poisson distribution was developed as a statistical model, which was called “the law of rare events” (also “law of small numbers”).
To recap, Poisson distribution is well suited to model rare events. Microbiological sampling at low microbial concentration is one example. Other examples include particle emission from radioactive elements, failure rate of machinery, rate of occurrence of rare diseases such as cancer and study of mortality (Engelhardt 1994¹⁵, Liddell 1984¹⁶). Confidence intervals of Poisson expected value have been extensively studied and the tables of confidence limits are readily available (Crow 1959¹⁷, Box 1978¹⁸, van Belle 2004¹⁹).
Several formulae have been developed by researchers to calculate confidence intervals of Poisson variable. With a spreadsheet such as EXCEL, it is straightforward to compute and compile a numeric table for confidence intervals. In the following, some of these formulae will be reviewed.
The following are some of the methods for obtaining the numerical values of confidence limits (lL and lU) of Poisson variables.
For confidence level of 1 – α/2, confidence interval can be obtained by using the following numerical methods.
Method 1: Direct calculation
For each of the number of occurrence k, select 2 Poisson parameters λL and λU so that the cumulative functions F (x, λ) of the Poisson probability density function are as follows:

Where, λL and λU are lower and upper confidence limits at 100(1 - α/2) % level.
Method 2: Calculation by chi square
There exists a link between confidence limits of Poisson distribution and chi square (χ2) distribution (Fisher 1935²⁰, Hald 1952²¹, Pearson 1976²², Liddell 1984¹⁶). From a chi square table, one can obtain the values of Poisson confidence limits. See formulae below.

Method 3: approximation for chi square
By Wilson-Hilferty approximation, chi square (χ²) values with n degree of freedom can be calculated by using z1-α/₂ value in normal distribution (Wilson 1931²³).
χ² is normally distributed about mean value of 1 – 2/(9k) with variance σ² = 2/(9k).


With this approximation, the lower and upper confidence limits can be calculated with the formulae using z value of normal distribution.

For a review of confidence interval calculations, please see (Sahai 1993²⁴).
A table of confidence intervals for the expected value of a Poisson random variable with different levels of confidence is in Appendix 1. Using the numerical values of confidence interval and the LOD, the values of LOQ can be assigned according to the proposed procedure discussed in previous section. Appendix 2 provides look-up tables for assigning LOQ at confidence levels of 95% and 99%.
Practical considerations
Figures 4 and 5 show variable non-zero results for some technologies, even for blanks with no microbes in the sample. In some scenarios, there will always be some microbial contamination and so blank samples are not possible to generate. A third possibility is that blanks with no microbes are perfectly feasible to generate but then equations (1) and (2) will result in the estimates LOD=LOQ=0 because the mean and SD of the blanks will be 0. Because of these technical issues with blanks, Figures 4 and 5 have used the term “blank” for illustrative purposes. We hope that using a “hypothetical blank” sample is a useful teaching tool, with Fig 4 analogous to Fig 1 for analytical chemistry. In the current practice of microbiological testing, LOD is not determined by comparing to a “blank” sample. Instead, regulatory guidelines specify a probabilistic approach for determining LOD by demanding a roughly 50%/50% proportion of growth/no growth test result. Briefly, LOD is determined in analytical chemistry by engineering metrology, while in microbiology by probability estimate.
There are many papers that describe how to find the LOD for CFU assays where the target is 5% positives - see e.g. Corry et al. 2007²⁵, Feldsine et al. 2002²⁶, Reiske 2019²⁷, Uhlig and Gowik 2018²⁸, Vencia et al. 2014²⁹, Yáñez et al. 2005³⁰. However, in practical microbiological tests, it will be very difficult to hit a target of 5% positive in preparing a batch of samples. That's why regulatory bodies have been realistic and recommended a more relaxed target of ~ 50% positives as we discuss in Option 1 above.
As discussed in previous sections, the determination of LOQ of a measurement method is mainly a task in statistics. In the field of microbiology there are additional complexity and technical challenges. The uncertainty and experimental difficulty in microbiological measurement are much higher than those in analytical chemistry. Because microbes are living organisms, the precise sampling and measuring are difficult to achieve. Specialized methods have been developed for enumerating microorganisms collected in a microbiological test.
In the regulatory guidelines for validating microbiological methods, 2 procedures are recommended for the determination of limit of detection (USP 2015²):
Procedure 1: prepare low concentration test samples such that the test results in plate counts show roughly 50% of growth in the collected samples and roughly 50% of non-growth in the rest of the sample. The limit of detection (LOD) is the average concentration calculated from all samples. This method yields an integral count in terms of colony forming unit (CFU), from which a concentration can be calculated from dividing the CFU count by the volume of the collected sample.
Procedure 2: MPN - Most Probable Number method, which is widely used in microbiological testing. In this method, low concentration a test sample is collected, and serial dilutions of the collected sample are made and incubated in a liquid growth medium. The pattern of growth and non-growth among the serial dilutions is noted and a MPN table is consulted to determine the concentration value of the original sample. This MPN method yields a concentration value (per unit volume or weight), not an integral count value.
Procedure 1 procedure is straightforward for a validation test, by judicially preparing samples to ensure both positive and negative results, a count (cfu) value can be readily obtained. But we have encountered a practical difficulty in describing Procedure 2 (MPN) for validation test as follows: in a test for LOD, the microbial concentration is usually quite low, it will not be practical to further dilute it for MPN determination. The MPN option is perhaps theoretically possible but not really practical. In a word, MPN is a suitable tool for estimating microbial density with a moderate concentration, but it is not practical for measurement of cfu counts in a purposefully-made low concentration sample such as LOD titer.
For the LOD determined by Procedure 1 (low concentration plate count), it is straightforward for LOQ assignment by the Poisson confidence and probability interval method. The CFU count value is used for finding the value of LOQ using the look-up table (see Appendix 2). Afterwards, this LOQ count value is divided by the sample volume to obtain the LOQ concentration value.
The method of using confidence and probability intervals to determine LOQ is still valid for the LOD values obtained by MPN method. Several approaches are suggested below to deal with this complication in the usage of the MPN method.
Confidence intervals tables for MPN have been published (Blodgett 2005³¹, Jarvis 2010³², FDA 2020³³) and can be used to assign LOQ values for a LOD value from the MPN test method. After finding a confidence interval, estimate of LOD by MPN method. Then, use a probability interval approach to set the LOQ so that Poisson count data generated with mean LOQ have a high probability of being above UCL and hence high confidence to be above the LOD.
Case studies for LOQ determination using count data
Case study 1: aerosolized bacterial testing
Aerosolized bacteria test is a standard task for microbiological method validation. This type of test is conducted inside an aerosol test chamber, which is an enclosure equipped with a nebulizer for aerosolizing bacterial sample, an air cleaner, and mixing fans for homogenizing the airborne bacteria concentration (Yeh 2022³⁴). The instrument under test and reference instrument (air sampler with growth media plate) are placed inside the aerosol test chamber, and a bacterial suspension is nebulized under controlled conditions to create a desired airborne bacterial concentration.
To illustrate the determinations of LOD and LOQ, we will do a case study of the data from an aerosolized bacteria test using Staphylococcus epidermidis. The instrument under test was a fluorescence based real time airborne microbial sensor Model BAMS, and the reference instrument was an air sampler with TSA growth medium plate Model BAS (both were from MicronView, Co. Ltd.) (Montenegro-Alvarado 2018³⁵). In this study, the new (alternative) microbiological method under test was the fluorescence microbial sensor BAMS; the compendial growth media reference method was the air sampler BAS. Both instruments were placed inside an aerosol chamber. The S. epidermidis aqueous solution was nebulized by a Salter nebulizer. For low concentration limit of detection test, the rate of bacterial nebulization was adjusted so that at least 50% of the samples collected by air sampler would show colony growth, per USP<1223> recommendation. The growth media plate count data from air sampler BAS from the dilution at which at least 50% of the samples are still positive are shown in the data table (Table 2) below using Option 1 of LOD determination per USP<1223> (2). For each replicate, 500 liter of air was collected by the air sampler, i.e. sample volume per replicate = 0.5 cubic meter.

This set of data yields a total plate count of (6 CFU)/(8 replicates) which yields the average 0.75 CFU/replicate, standard deviation = 0.71 CFU/replicate, and coefficient of variation CV = 0.94. It is observed that the number of replicate (n = 8) satisfied both the recommendation by USP<1223> and the requirement imposed by negative binomial model mentioned earlier in this paper, as shown in Table 1.
The limit of detection thus obtained is as follows:
LOD = (6 CFU)/ (8 replicates) = 0.75 CFU/0.5m³ = 1.5 CFU/m³.
Consulting Appendix 2 with LOD=6 CFU/ (8 replicates), the limit of quantification can be determined as follows:
LOQ (at 90% confidence level) = 20.7 CFU/ (8 replicates) = 5.2 CFU/m³.
Case study 2: comparison tests of air samplers
Air sampler measurement is an essential task in microbiological environmental monitoring process. Because of the high variability of microbial distribution in the environment compounded by the variations in sampler performance, careful tests are needed to ascertain the suitability of an air sampling plan regimen (Eaton 2021³⁶). In the context of environmental microbiology, the measurement variability can be roughly classified into 2 categories: intra-species variability, which is that of the measurements of the concentrations of the microbes belonging to the same species but measured at different times and by different instruments; and, inter-species variability, which is that of the measurements between different microbial species.
As elucidated by Sharp et al⁴, the requirement for the number of replicates in a testing for a desired level of false negative rate is related to the coefficient of variation (CV) of the measurement. Therefore, the detailed information on the sources of test variabilities is of significant utility in sampling planning. In the following, we will use the published air sampling data (Eaton 2021³⁶) as an illustrative example for analyzing measurement variabilities.
In the paper of Eaton (Eaton 2021³⁶), 2 species of bacteria (Bacillus atrophaeus spores and Staphylococcus epidermidis) were sampled by 2 air samplers of different manufacturers. The test data (Table A1 of Eaton 2021³⁶) are reproduced below in Table 3.

From the above data, the coefficients of variation (CV) of different measurements were calculated and listed below in Table 4.
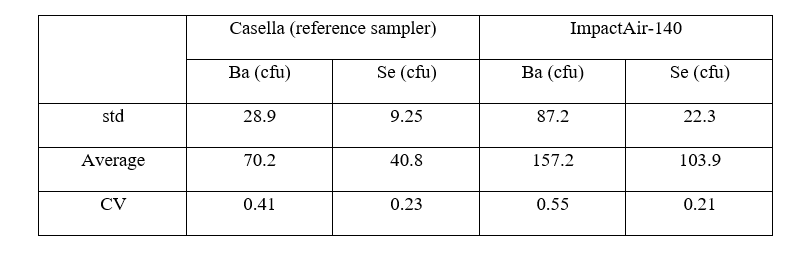
Some technical assessments can be readily derived from these carefully planned tests. (1) For the same bacterial species, CV’s of 2 samplers are similar, indicating comparable performances. We can conclude that the Intra-species variability by using those 2 samplers was a stable statistical parameter. (2) There was a marked difference in CV between Ba and Se species, possibly due to the dispersions in bacterial sizes and collection efficiency of the samplers. The conclusion would be that the Inter-species variability between these 2 species of bacteria might be worthy of consideration in the planning of environmental monitoring testing. For example, in an environment where the microbe species with higher CV (e.g. Ba) is more prevalent, one might want to increase the number of replicates in testing to accommodate the higher CV value.
One side note: from statistical consideration, the information on the measurement variabilities (both intra- and inter-species variabilities) requires detailed tests, such as this study by Eaton (Eaton 2021³⁶), at high enough microbial concentration level so that a meaningful statistical assessment is feasible. The assessment thus obtained will be useful in the planning for tests for lower microbial concentration levels for LOD testing.
Case study 3: air sampler tests in surgical clothing test chamber
Ljungqvist et al (Ljunqvist 2024³⁷) did a comparison study of air samplers in testing surgical clothing in a disposal test chamber. Some of their air sampler data were selected here to illustrate the determination of LOD and LOQ, as follows (Table 2, Ljungqvist 2024³⁷) in Table 5.

From the above data, the coefficients of variation (CV) of different measurements were calculated and listed below in Table 6.

Technical assessments: (1) In this data example, for the aerobic cfu counts, CV value is 0.68. In this case, if the false negative rate (β) of 0.05 is desired, then a minimum of 4 replicates in testing is required for LOD testing. As seen in the data table, this requirement had been satisfied. (2) Considering the average of this set of aerobic cfu counts as LOD ≈ 2, from the look-up table in Appendix 2, a LOQ = 13 can be assigned at 95% confidence level.
An additional comment on the utility of LOQ: in microbiological laboratory practice, there is a convention for a range of the most suitable number of colonies on growth media plates for counting (Tomasiewicz 1980⁷). We propose that the concept of LOQ might be used to give this suitable number of colonies for plate counting a statistical interpretation. We submit that the lower level of this suitable number of colonies could be defined as a numerical value, above which the quantitative assurance can be assigned a statistical confidence level (e.g. at 95%). Tomasiewicz et al suggested a range of 25 to 250 colonies/plate as the suitable number for plate counting. Let’s analyze the suggested lower number of 25 in the context of LOD and LOQ: in practical microbiology laboratory testing, a LOD level of 1 to 5 CFU counts per plate would be a reasonable occurrence; in this case, consulting Appendix 2, a LOQ = 25 at a confidence level of 99% can be assigned, Thus we could offer a statistical interpretation of Tomasiewicz proposed range as between limit of quantification (LOQ) and too-numerous-to-count (TNTC).
CONCLUSION
We propose a procedure for determination of limit of quantification (LOQ) based on Poisson confidence interval and probability intervals. The choice of using confidence interval of the LOD and then a probability interval for the LOQ was motivated both by the broad regulatory guideline and by the statistical theoretic considerations. In our proposal for LOQ in plate count data of microbiological tests, the basic methodology is similar to that of analytical chemistry. Since microbiological plate count data are discrete, close to zero and exhibit high variability, it is necessary to use a different statistical treatment than normal distribution formulation commonly used in analytical chemical data processing. For this purpose, a Poisson distribution model is used in this proposal for confidence and probability interval calculations. To facilitate practical implementation of our proposal for LOQ determination, we have provided look-up tables for Poisson confidence intervals (Appendix 1) and probability intervals (Appendix 2). It has been pointed out that microbiological plate count data (colony forming unit, CFU) display over-dispersion as compared to Poisson model (Sharp 2023⁴). We duly take this extra-variability into consideration and propose a criterion of number of replicates requirement in a microbiological test to mitigate its impact. The criterion was derived from a negative binomial model for different levels of variabilities (quantified by coefficient of variation, CV).
Acknowledgements
The authors wish to thank MicronView for permission of the usage of aerosol bacteria test data in this article. The authors also wish to thank EJPPS for permission to use published data from its past issues in this work.
Conflict of Interest
J.P.J. is a consultant of MicronView, LLC; he declares that he has no other conflict of interest. A.E.P. declares that he has no conflict of interest.
References
1. European Pharmacopoeia Chapter 5.1.6. (2017).
2. USP<1223> “VALIDATION OF ALTERNATIVE MICROBIOLOGICAL METHODS”, 2015.
3. PDA technical Report TR33, Evaluation, Validation and Implementation of Alternative and Rapid Microbiological Methods. 2013.
4. Sharp, Julia L.; Parker, Albert E.; Hamilton, Martin A. Calculating the limit of detection for a dilution series. Journal of Microbiological Methods, 2023 April, 208(2):106723.
5. Currie, L. A. Foundations and Future of Detection and Quantification Limits. American Statistical Association Proceedings of the Section on Statistics and the Environment, 1996, 1 - 8.
6. Whyte, W. Formal methods of selecting monitoring locations and control levels, European Journal of Parenteral and Pharmaceutical Sciences, 2022, 27(1).
7. Tomasiewicz, Diane M.; Hotchkiss, Donald K.; Reinbold, George W.; Read, Ralston B., and Hartman, Paul A.. The Most Suitable Number of Colonies on Plates for Counting, Journal of Food Protection 1980, 43(4), 282-286.
8. Kaiser, H. Zum Problem der Nachweisgrenze, Zeitschrift für Analytische Chemie, 1965, 209, 1-18.
9. Kaiser, H. “Guiding concepts relating to trace analysis. Pure Appl. Chem., 1973, Vol. 34, No. 1, pp. 35-62.
10. Keith, L. H., Crummett, W; Deegan, J Jr; Libby, R A; Taylor, J K; Wentler, G. Principles of Environmental Analysis. Anal. Chem., 1983, 55(14): 2210-2218.
11. Clinical and Laboratory Standards Institute. Protocols for Determination of Limits of Detection and Limits of Quantitation, Approved Guideline. CLSI document EP17. Wayne, PA USA: CLSI; 2004.
12. Miller, Michael, Encyclopedia of Rapid Microbiological Methods, Vol.4, PDA, 2013.
13. Sutton, Scott; Accuracy of plate counts. Journal of Validation Technology, Summer 2011.
14. Theodorsson, Elvar; Limit of detection, limit of quantification and limit of blank, EFLM Zagreb, 2014.
15. Engelhardt, M. E. Events in Time: Basic Analysis of Poisson Data, EGG-RAAM-11088, 1994.
16. Liddell, F.D.K. Simple exact analysis of the standardised mortality ratio. Journal of Epidemiology and Community Health, 1984, 38, 85-88.
17. Crow, Edwin L.; Gardner, Robert S. Confidence intervals for the expectation of a Poisson variable. Biometrika, 1959, Dec., Vol. 46, No. 3/4, pp. 441-453.
18. Box, George E. P.; Hunter, William G.; Hunter, J. Stuart; “Statistics for Experimenters –An Introduction to Design, Data Analysis, and Model Building” John Wiley & Sons 1978.
19. van Belle, Gerald; Lloyd Fisher, Patrick J. Heagerty; Lumley, Thomas; Biostatistics: A Methodology for the Health Sciences, 2nd Edition. Wiley 2004.
20. Fisher, RA. The mathematical distributions used in common tests of significance. Econometrica, 1935, 3:353-65.
21. Hald, A. Statistical Theory with Engineering Applications. John Wiley and Sons, New York, 1952, pp 722-723.
22. Pearson, E.S.; Hartley, H.O. Biometrika tables for statisticians. Vol. I, 3rd ed. London: Biometrika Trust, 1976.
23. Wilson, Edwin B.; Hilferty, Margaret M. The distribution of Chi-square, Proc. Natl. Acad. Sci. USA. 1931; 17(12): 684–688.
24. Sahai, H.; Khurshid, A. Confidence Intervals for the Mean of a Poisson Distribution: A Review. Biometrical Journal, 1993, 35 (7), 857-867.
25. Corry, J. E. L.; Jarvis, B.; Passmore, S.; Hedges, A. A critical review of measurement uncertainty in the enumeration of food micro-organisms. Food Microbiology, 2007, 24(3), 230–253.
26. Feldsine, P.; Abeyta, C.; Andrews, W. H. AOAC INTERNATIONAL Methods Committee guidelines for validation of qualitative and quantitative food microbiological official methods of analysis. Journal of AOAC INTERNATIONAL, 2002, 85(5), 1187–1200.
27. Reiske, H. The How and Why of Limit of Detection. (2019). Available at: https://bitesizebio.com/44092/how-to-calculate-the-limit-of-detection-for-an-assay-and-why youd-want-to/. Accessed 06/20/2022.
28. Uhlig, S.; Gowik, P. Efficient estimation of the limit of detection and the relative limit of detection along with their reproducibility in the validation of qualitative microbiological methods by means of generalized li near mixed models. Journal of Consumer Protection and Food Safety, 2018, 13(1), 79–87.
29. Vencia, W., Nogarol, C., Bianchi, D. M., Gallina, S., Zuccon, F., Adriano, D., Gramaglia, M., & Decastelli, L. Validation according to ISO 16140:2003 of a commercial real-time PCR based method for detecting Campylobacter jejuni, C. coli, and C. lari in foods. International Journal of Food Microbiology, 2014, 177, 78–80.
30. Yáñez, M. A.; Carrasco-Serrano, C.; Barberá, V. M.; & Catalán, V. Quantitative detection of Legionella pneumophila in water samples by immunomagnetic purification and real time PCR amplification of the dotA Gene. Applied and Environmental Microbiology, 2005, 71(7), 3433–3441.
31. Blodgett, Robert J. Upper and Lower Bounds for a Serial Dilution Test. Journal of AOAC International, 2005; Vol. 88, NO. 4.
32. Jarvis, B.; Wilrich, C.; Wilrich, P.-T. Reconsideration of the derivation of Most Probable Numbers, their standard deviations, confidence bounds and rarity values. Journal of Applied Microbiology, 2010,109, 1660–1667.
33. FDA 2020, “BAM Appendix 2: Most Probable Number from Serial Dilutions” (https://www.fda.gov/food/laboratory-methods-food/bam-appendix-2-most-probable-number-serial-dilutions#table1 ).
34. Yeh, Kenneth B.; Setser, Bradly, Aerosol Test Chamber Perspective, Front. Bioeng. Biotechnol., 2022, Vol. 10.
35. Montenegro-Alvarado, José-Miguel; Salvas, Joanny; Weber, Jeffrey; Mejías, Soraya; Arroyo, Ramón, Pfizer Case Study: Rapid Microbial Methods For Manufacturing Recovery After Hurricane María. Pharmaceutical Online, July 2018.
36. Eaton, Tim; Microbial Air Samplers for Meaningful Cleanroom Environmental Monitoring, European Journal of Parenteral and Pharmaceutical Sciences, 2021, 26(3).
37. Ljungqvist, Bengt; Nordenadler, Johan and Reinmüller, Berit ; A COMPARATIVE STUDY OF A STANDARD SLIT-TO-AGAR SAMPLER AND A REAL-TIME BACTERIAL DETECTOR, European Journal of Parenteral and Pharmaceutical Sciences, 2024, 29(1).
38. Natrella, Mary Gibbons, Experimental Statistics, NBS Handbook 91, US Department of Commerce 1963.
Appendixes
Appendix 1

Appendix 2


Appendix 3
After blank data are collected at the completion of Step 1, consider an (1 – α) upper confidence limit (UCL) for the true mean of the blanks (µblank) as UCL = xblank + ks as in equation (1) where xblank is the sample mean, s is the SD of the blank samples (sblank) and

is the multiplier. This means that

When α = 0.015 and n=2, 3, 4 then the t-quantile tn-1,1-α=21.2, 5.6, 3.9 respectively in which case k =15.0, 3.3, 1.9, so k ≤ 3.3 whenever n ≥ 3. This means that setting k=3.3 assures that UCL= xblank + ks has a confidence level of at least 98.5% as long as there are at least n=3 blank samples.
After LOD data are collected at the completion of Step 3, consider an (1 – α) upper confidence limit (UCL) for the true mean of the LOD samples (µLOD) at concentration c* as UCL = xLOD(c*)+k*s with k* = tn-1,1-α/√n. When k=3.3 in equation (1), then equation (2) becomes xLOQ = xLOD + 6.7s ≈ xLOD(c*)+6.7s with under the assumption that sblank and sLOD are estimating the same true variance. When α = 0.004 and n=2, 3, 4 then the t-quantile tn-1,1-α=79.6, 11.1, 6.3 respectively in which case k* =56, 6.4, 3.2, so k* < 6.7 whenever n ≥ 3. This means that setting k*=6.7 assures that UCL= xLOD(c*)+6.7s for the true LOD has an approximate confidence level of at least 99.6% as long as there are at least n=3 blank samples.
Now consider possible values for the LOQ (µLOQ) such that p% of the data to be generated with true mean µLOQ have a high probability (1 – α) of being greater than the true LOD µLOD. This is accomplished by finding a value of µLOQ such p% of the data with mean at µLOQ have probability (1 – α1) of being above the (1 – α2) UCL for µLOD. Then p% of the data will have probability (1 – α1)(1 – α2) of being above µLOD. We showed above that P(µLOD <UCL = xLOD + 3.3s) = 0.985 (=1 – α2) when n≥3. And using the tolerance interval approach due to Natrella (38), setting µLOQ = UCL +3.3s assures that

Therefore,

which implies that
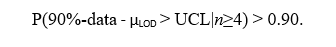
A similar argument can be used to show that

Authors
Jianping Jiang 1, Albert E. Parker2,3
¹ MicronView, LLC.
² Center for Biofilm Engineering, Montana State University, Bozeman, MT USA
3 Department of Mathematical Sciences, Montana State University, MT USA
Corresponding Author: J.P. Jiang
MicronView, LLC.
2300 Highway 365
Suite 110
Nederland TX, 77627 USA
Email: j.p.jiang@hotmail.com
Telephone: (520) 326-7998




Comments