- EJPPS

- Mar 14, 2022
- 18 min read
Updated: Mar 30, 2022
Peer Review Article | Open Access | Published 25th March 2022
Formal methods of selecting monitoring locations and control levels
W Whyte | EJPPS | 271 (2022) |https://doi.org/10.37521/ejpps.27102 Cite this article | Click to download pdf
The following article has been published in the book Cleanroom Testing and Monitoring. It was originally written by Dr Whyte, with the assistance of Tim Eaton and Joe Gecsey, for publication in the EJJPS, but owing to the demands of publishing it was redirected to become an annex in the book. However, the subject of the annex is considered to be of interest to readers of the EJPPS and is reproduced here. It was also considered useful to alert readers who are concerned with the testing and monitoring of cleanrooms about the publication of the book.
Editor
Abstract
It is necessary to determine locations in a cleanroom where airborne concentrations of particles and microbe-carrying particles (MCPs) should be monitored. It is also necessary to determine the concentrations of airborne contamination that should not be exceeded during manufacturing operations, ie. the alert and action control levels. Both these requirements can be ascertained by simple and informal means. However, should a formal approach be required, the monitoring locations can be determined by a risk assessment, and the control levels by a statistical method.
Key Words: Monitoring, airborne particles, control levels, pharmaceutical, cleanrooms
Introduction
Methods for monitoring cleanrooms to ensure they correctly function and provide the required standards of cleanliness have been previously discussed 1. However, two topics were highlighted for further consideration, namely:
The selection of locations for monitoring airborne contamination, and,
The establishment of control levels that give the concentrations of airborne contamination that should not be exceeded.
Monitoring locations are best obtained by means of a risk assessment that identifies locations where there is the greatest risk to the product or process. A simple informal risk assessment method can be used of the type that is briefly discussed in Annex A of the book 2. However, to obtain the best results, a formal risk assessment should be carried out, and a suitable method is discussed in this article.
Concentrations of airborne contamination that should not be exceeded during monitoring need to be established. In cleanrooms, this is often carried out by setting limits that are known as control levels. The two control levels that are commonly used are ‘alert’ and ‘action’ levels. The meaning of these control levels, and how they can be informally chosen, has been discussed in Annex A in the book ‘Cleanroom Testing and Monitoring’ 2. In this article, formal statistical approaches are described.
The formal methods of choosing monitoring locations and control levels discussed in this article are applicable to both airborne particles and microbe carrying particles (MCPs).
Choice of locations for monitoring airborne contamination
When classifying a cleanroom according to ISO 14644-1: 2015 3, the airborne particle concentrations must be measured at locations evenly spread about the cleanroom. However, when monitoring airborne particles or MCPs, measurements should be carried out at locations where airborne contamination is most likely to cause product contamination. The main locations are critical locations where product or process is exposed to deposition of contamination from the surrounding air. However, consideration should also be given to critical control points (CCPs) where the transfer of airborne contamination to critical locations is controlled, as well as sources of high concentrations of airborne contaminants.
Monitoring locations can be informally chosen from knowledge of the functioning of the cleanroom and the manufacturing process. However, a more formal approach may be required and Hazard Analysis and Critical Control Point (HACCP) 4 and Failure Mode and Effect and Criticality Analysis (FEMCA) 5 are risk assessment methods most frequently used in cleanrooms. Their general application to contamination control in cleanrooms is discussed in more detail elsewhere 6.
Types of monitoring locations
There are three types of locations that have a high potential risk for causing contamination of a product or process. These may need to be monitored and are the following types:
Critical locations: These are locations where critical surfaces such as product, components, and processes are exposed to direct deposition of contamination from the surrounding air. This type of location is likely to give the greatest risk of contamination to product or process and is usually the best location to monitor.
Critical control points (CCPs): These are locations where the transfer of airborne contamination to the product or process is controlled, such as the entrance and exit of an isolator or minienvironment. The CCPs selected for monitoring should be where a failure of a control mechanism is likely to cause significant product contamination. Special attention should be paid to the concentration of the contamination challenge and the amount of transfer across the control point.
Sources with high dispersion rates: These may be sources in a cleanroom or clean zone, such as a machine or person, with a high dispersion rate of airborne contamination that can be easily transferred to critical surfaces. Special attention should be paid to the concentration of airborne contamination at the source and the ease of transfer of contamination to a critical surface. If a substantial risk is identified, then monitoring should be carried out close to the source and on the air transfer pathway to the critical surface.
Calculation of the risk of airborne contamination at possible monitoring locations
The first step of the formal method of determining monitoring locations is to choose locations that have a potential for causing airborne contamination of critical surfaces. These will usually be one of the three types of monitoring locations that have been discussed in the previous section. The risk at these possible monitoring locations should be assessed to find those with the highest potential risk to critical surfaces. This can be determined by a risk assessment that takes account of the probability and severity of the risk factors of contamination. The risk factors that determine the amount of airborne contamination at a potential monitoring location can that be transmitted to a critical surface are as follows.
Concentration of airborne contamination: the higher the concentration of airborne contamination (particles or MCPs) at a potential monitoring location, the higher is the likelihood of contamination occurring at a critical surface. Depending on where the risk comes from, the airborne contamination can be (a) the concentration next to a critical surface (b) the concentration that challenges a CCP, or (c) the concentration at a source that disperses large quantities of airborne contamination.
Transfer coefficient: if monitoring locations are remote from the critical surface, then the proportion of airborne contamination that is likely to be transferred to the critical surface, i.e. the transfer coefficient, should be included in the risk assessment. The transfer coefficient can be determined by the following Equation 1.

Surface area: this is the area of the critical surface that is exposed to airborne deposition. The larger the surface area is, the greater the potential for contamination.
Time: this is the time the critical surface is exposed to airborne deposition. The longer the critical surface is exposed, the greater the potential for contamination.
Risk scores are assigned to each of the risk factors, and Equation 2 is used to obtain a risk rating which can identify locations with the highest potential risk to product, and where monitoring might be carried out.
Equation 2
Risk rating = airborne concentration x transfer coefficient x surface area exposed x time exposed
To solve Equation 2, risk scores are assigned to the four risk factors. Risk scores can be descriptors of the importance of the risk and can be considered as surrogates of the actual values of the risk factors. Descriptors of risk can be, for example, ‘high’, ‘medium’, ‘low’ and ‘zero’, which are given a risk score of ‘3’, ‘2’, ‘1’ and ‘0’, respectively, that is inserted into Equation 2. There are a variety of methods that can be used for scoring risk factors 6 and a suitable method should be used. If actual values of the risk factors are available, these can either be allocated a descriptor as a risk score, or the actual values used.
Example of a risk assessment
Given in Table 1 and Table 2 are the results of an example of a risk assessment carried out to select monitoring locations in an isolator. The isolator contains a filling line for containers and has been previously described in articles written by Tim Eaton 7, 8, and these articles should be consulted.
The risk to critical surfaces in the isolator from direct airborne contamination is included in Table 1, and the risk to product from CCPs at the entrance and exit of the isolator is calculated in Table 2. No large sources of airborne contamination were present in the isolator and, therefore, they are not included in the risk assessment. The first two columns of both tables give a list of possible monitoring locations. These locations are given in order of manufacturing i.e. from introduction of empty containers into the isolators, to the exiting of filled and stoppered containers.
In this risk assessment, risk scores of the descriptor type were not used. Risk scores of the likely concentration of airborne contamination were based on the amount of activity of personnel and equipment at each location. Had the ventilation system varied along the length of the isolator then the risk from the amount of activity could have been adjusted by the different quality of ventilation. However, this was considered to be unnecessary. Activity is scored in the range between 1 and 2. Where there is no activity, the risk score is 1. Where there is activity, the risk is scored between 1 and 2, and determined by the activity time as a percentage of the total time, e.g. activity at a location for 10% of the total time is given a score of 1.1.
Actual values of the critical surface area (cm²) of the container neck opening, needles, and stoppers exposed to airborne contamination were used. However, when containers are stoppered and exit the isolator, they are stoppered and the surface area exposed to contamination is considered to be zero. The exposure times (minutes) of the critical surfaces to contamination were also obtained and given in Table 1. The transfer coefficient was not included in this risk assessment as it was considered to be reasonably constant within the isolator and not needed in the risk assessment. The three types of risk scores were multiplied together to obtain the risk rating from each step in the manufacturing process.
Table 1 Risk assessment of locations in an isolator

Table 2 gives an assessment of the risk to product from the transfer of airborne contamination from outside the isolator and across the CCPs to the containers. At the entrance to the isolator, the contamination challenge comes from an interfacing supply tunnel which was ventilated with UDAF and there was no activity within it, and an airborne contamination risk score of 1 is allocated. At the exit there is an interfacing open-access UDAF workstation that contains crimping equipment, and the airborne concentration is likely to be higher and a risk score of 2 is allocated. The transfer coefficient was estimated to be no worse than 0.01 at both the entrance and exit. The risk scores of the time the container was exposed to contamination were the actual values, which was 10 minutes at both the entrance and exit to the isolator. The area of the container neck opening was 2cm² but at the exit the containers were stoppered and, therefore, the area of the container neck exposed to airborne contamination was zero. Using this information, the two risk ratings of the CCPs were calculated by use of Equation 2 and are given in Table 2.
Table 2 - Risk assessments of importance of critical control points

Typically, monitoring will be mainly carried out next to critical surfaces where the greatest amount of direct contamination is expected from the surrounding air. However, there may also be important critical control points, as well as sources that disperse high concentrations of airborne particles and MCPs, and these should also be considered as possible monitoring locations. To decide which locations should be selected for monitoring, a threshold value for the risk rating is used, and any location above that value is selected. The threshold value will vary according to the type of risk assessment and the number of monitoring locations to be used. In the example shown in Table 1 and Table 2, when the threshold value of the risk rating is taken as four, three locations exceed this value (locations 1, 2 and 9) and these can be selected for monitoring. If a risk rating score of ten is used as the threshold, two locations exceed this value (locations 1 and 9). It was noted that the monitoring locations that were selected were where contamination was caused by direct deposition from the surrounding air, and no CCPs, or sources of high dispersion of contamination, were included.
In cleanrooms that provide a background to a clean air device, one or two locations that present the greatest risk to product might be monitored. These locations are the ones that have a combination of high particle concentrations and likelihood that the contamination can be transferred to product or process. Information about the particle concentrations in the cleanroom will have been gathered during the cleanroom classification and this information can be combined with the likelihood of transfer of particles to the product or process in order to select monitoring locations.
A risk assessment of other general support cleanrooms can be carried out to decide which location, or locations, are considered to give the highest risk to product and where monitoring should be carried out. This is typically one monitoring location per cleanroom.
Selection of control levels of contamination concentrations
Locations are monitored in cleanrooms to ensure that maximum limits of airborne concentrations of particles or MCPs are rarely exceeded. The method commonly used to set these limits is by using control levels called ‘alert’ and ‘action’. The action level is the concentration of contaminants that should not be exceeded and, if it is, there should be immediate action to rectify the problem. This is, typically, the maximum airborne contamination concentration in the chosen ISO class, or in regulatory documents such as Annex 1 of the EU GGMP 9, or FDA Guidance 10. Alternatively, it can be the concentration that is unlikely to be exceeded in a cleanroom or clean zone where the actual operational particle concentration has turned out to be considerably lower than the design requirement. An alert level is usually an airborne concentration that is greater than normally found in the cleanroom or clean zone. It may give an early warning of a drift to an unacceptable condition and, when encountered, requires increased vigilance or, perhaps, an investigation or corrective action.
Alert and action levels can be informally or empirically selected. However, this annex discusses how the sample can be formally obtained by means of statistics, and the statistical methods will now be discussed.
Use of statistics to set control levels
Airborne concentrations that should not be exceeded during monitoring can be obtained by a method based on Statistical Process Control (SPC) 11. This statistical technique is routinely employed in general manufacturing industry to control and improve the quality of product and can be used in cleanrooms.
Before discussing how SPC can be applied to selecting action and alert control levels, some basic statistics should be reviewed. Shown in Figure 1 is the well-known Normal statistical distribution with its familiar bell shape. The mean average value (µ) is at the centre peak, and the frequency of occurrence of the results before and after the mean is shown to tail off equally in both directions. The extent of the spread of the results is obtained from the calculation of the standard deviation (σ), and the greater the standard deviation, the greater the spread of the results.
As shown in Figure 1, provided by Daniel Styne, in a Normal distribution the results contained within one, two, and three standard deviations of both sides of the mean are about 68%, 95%, and 97.3% of the results, respectively.

The results of the airborne concentration of particles and MCPs in many cleanrooms will conform reasonably well to a Normal distribution, although in some cleanrooms other statistical distributions, such a Poisson, log-normal or negative binominal, may give a better fit. It is reasonable, when first setting up the monitoring of airborne particles, to assume a Normal distribution and then to investigate the need for a better statistical distribution when more results are gathered. If a statistical distribution that best fits the results is used, a more accurate prediction of the concentration of airborne contamination at a given probability of occurrence can be obtained, and this will allow the control limits to be more accurately set.
Statistical distributions of airborne counts of contamination found in cleanrooms
Shown in Figure 2 is a typical distribution of ≥0.5µm airborne particles measured at a single location in an ISO Class 7 cleanroom. The mean is 115,000/m3 and the standard deviation is 73,000/m3. A considerable variation in the counts can be seen, and the count distribution conforms reasonably well to a Normal distribution, with a bell-shaped curve of the type shown in Figure 1. However, it can be seen that it varies from a perfect Normal distribution in having a positive skew and outliers with high counts. It is normal to find outliers with high counts in cleanrooms, and they should not be dismissed as technical mistakes caused by the sampling method, or removed from the results, unless there is a sound technical reason.
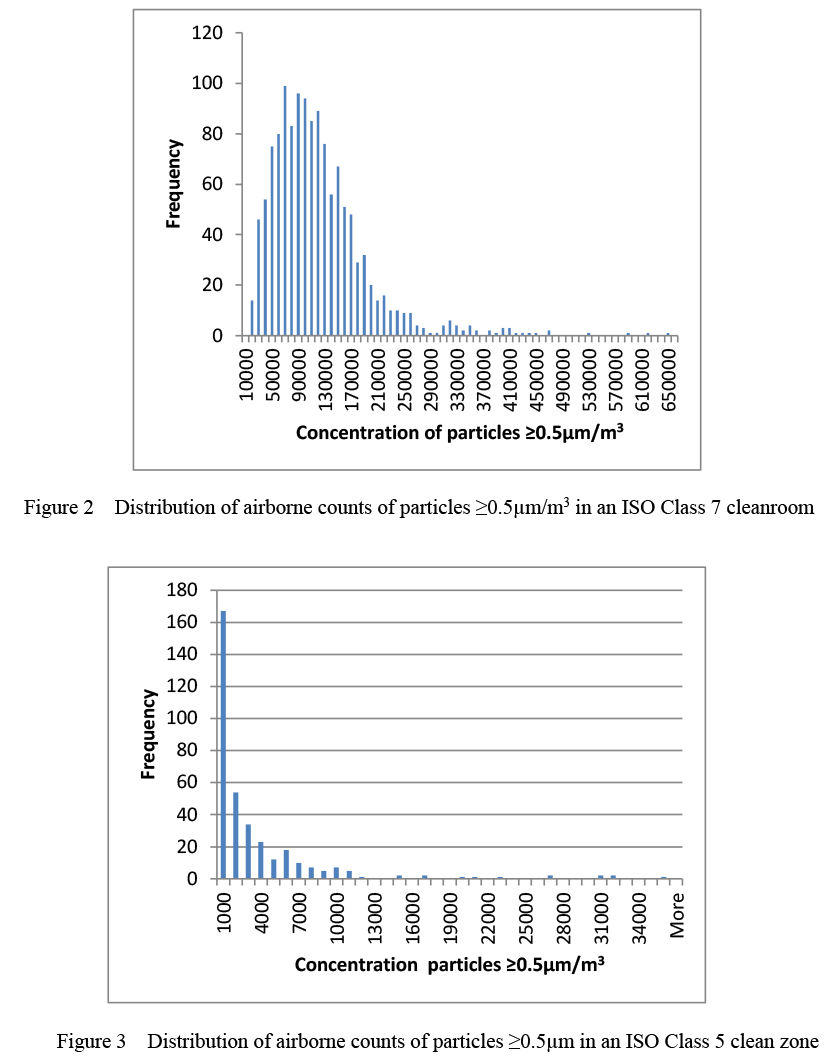
Shown in Figure 3 is the frequency of counts of ≥0.5µm particles found at a single location in an ISO Class 5 clean zone. The mean is calculated to be 3000/m3 and the standard deviation 5200/m3. This cleaner zone has many zero counts, which causes the left-hand side of the distribution to deviate from the symmetry found in a Normal distribution. It is common in better controlled ISO Class 5 zones to have more zero counts and the distribution to be even more asymmetric. Also, in the same manner as shown in Figure 2, the right-hand side of the distribution has an extended tail with high outlying counts. Very similar distributions to those shown in Figures 2 and Figure 3 are obtained when the airborne concentrations of MCPs are measured.
Setting alert and action levels using statistical distributions
As previously discussed, the standard deviation of a distribution of airborne counts shows how much the counts are spread out from the mean concentration, and the higher the standard deviation, the further the results will spread from the mean. As shown in the Normal distribution in Figure 1, two standard deviations on each side of the mean should contain 95% of the total number of sampling results, and these values are called the 95% upper and lower confidence limits (95% UCL and 95% LCL). Three standard distributions on each side of the mean will contain about 99.7% of the results.
Both the 95% and 99.7% confidence limits include counts that are above and below the mean. However, counts below the mean are unimportant in the context of the control of contamination in a cleanroom and can be disregarded; a better approach is to only consider counts above the mean. The counts that are beyond two standard deviations above the mean of a Normal distribution contain the highest 2.3% of the total results, which is 1 in 44 counts. Counts beyond three standard deviations above the mean contain 0.14% of the total counts, which is 1 in 740 counts. Using this information, there are two alternatives that can be used to set action and alert levels.
(a) The action value can be set at the maximum particle or MCP concentration set by ISO 14644-1, Annex I of the EU GGMP, or the FDA Guidance. This is the value that has been used to design the cleanroom or clean zone. The alert level can then be set at two or three standard deviations above the mean particle concentration to show when the count is above a level that is expected owing to the natural variation of the counts. It may be necessary, if insufficient results are available, to estimate the mean and standard deviation of the counts and improve these estimates through time.
If the results given for an ISO 7 cleanroom in Figure 2 are considered, the action value can be set at the limits for an ISO Class 7 cleanroom in the operational state. This is 352,000/m³ for particles ≥0.5µm. The alert level can then be set at two times the standard deviation above the mean, which is the 95% UCL, and is 115,000 + (2 x 73,000) = 261,000. Alternatively, it can be set at three standard deviations above the mean, which is the 99.7% UCL, and given a value of 334,000. However, the latter method will result in less control of airborne contamination, although it may be useful where continuous monitoring gives so many results that there is excessive breaching of the control levels.
(b) Set the value of the action level at an airborne particle concentration that is rarely exceeded in the cleanroom. The action level that is usually suggested by the Statistical Process Control method, and often adopted in cleanrooms, is three standard deviations above the mean, which is 99.7% UCL. In this situation, the alert value is often set at two standard deviations above the mean, which is at the 95% UCL. Using the results shown in Figure 2 and the calculation discussed in the previous paragraph, the action value would be 115,000 + (3x 73,000) = 334,000, and the alert value would be 261,000.
Control charts
Control charts are considered to be part of the Statistical Process Control method. However, if particle concentrations are continuously monitored, there is likely to be more information than can be dealt with by control charts. The computational ability of a Facility Monitoring System (FMS) is required to deal with the large quantity of results that need to be analysed and stored. Control charts are useful when there are a smaller number of results.
The method of analysis used by a FMS is similar to that used by control charts, and it is useful to visualise and understand the SPC method by means of a chart, and this will now be discussed. Should a fuller description be required about different types of control chart and their use, it will be found in one of many books written about SPC 11. Information about control charts is also available in the ISO 7870 series of standards 12.
A simple example of a control chart used during periodic monitoring of airborne particle concentrations and carried out during operations in an ISO Class 7 cleanroom is shown in Figure 4. This shows the airborne particle concentration when particles ≥0.5µm are sampled monthly.
The action level is the maximum limit of an ISO Class 7 cleanroom, which is 352,000/m3 for particles ≥0.5µm. Sampling in the cleanroom during operations showed that the particle concentrations conform reasonably well to a Normal distribution, with a mean average of 116,000/m3 and a standard deviation of 32,000. This standard deviation is smaller than typical values found in cleanrooms but has been chosen to illustrate what might happen when an alert level is exceeded. The alert level is set at two times the standard deviation greater than the mean, and is 116,000 + (2 x 32,000) = 174,000. The average, alert and action levels are shown in Figure 4.

For the set of data shown in Figure 4, it can be seen that the action level is never breached, but the alert level is breached once at the 31st count. This breach might have been caused by the natural variation found in counts as, when an alert level is set at two standard deviations above the mean value, a breach is expected, on average, about once in 44 counts. This breach was, therefore, noted and observation of the next few results heightened. No further breach occurred in the next few results, and no investigation was considered necessary.
Setting alert and action levels by means of a non-parametric distribution
The previous section of this chapter discusses how control levels can be set by a statistical distribution that fits the airborne concentrations measured in the cleanroom. However, accurate control values will only be obtained if the results fit well to a known type of statistical distribution. This is often not the case, and an approach that overcomes this problem is to assume that the particle counts do not conform to any standard type of statistical distribution but are distributed in the manner that they are actually found. This type of distribution can be called a non-parametric distribution.
Control levels of airborne concentrations can be set at the upper percentiles of the results of a non-parametric distribution. A percentile is the percentage of counts obtained in the situation being observed which, in this case, are the concentrations of airborne contamination in a cleanroom. If, for example, 1,000 readings of airborne particle counts are obtained and they are placed in order from lowest to highest count, the 950th, 990th, 995th, and 999th count is the 95th, 99th, 99.5th or 99.9th percentiles, respectively. These percentiles can be considered to be equivalent to the UCLs of a statistical distribution and, for example, the 95th percentile would be equivalent to the 95% UCL of a statistical distribution, and so on. Percentiles can be used in the same way as UCLs were previously used to set the control levels.
In a typical cleanroom, the action level could be set at the concentration limit given in ISO 14644-1: 2015, or an appropriate regulatory document. Alternatively, if the cleanroom is much cleaner than this design value, a suitable percentile value, such as the 99.9th percentile, could be used. The alert value in both situations could then be set at a suitable upper limit such as the 95% or 99% percentile.
The non-parametric approach to setting control levels is simpler than using the mean and standard deviation of a statistical distribution. However, this does not mean that it is less scientifically correct. It uses the actual distribution of the particle counts and is, therefore, more likely to be correct and accurate, and is the best approach in most situations.
Acknowledgements
The above article is from the book ‘Cleanroom Testing and Monitoring’ and is published with the kind permission of the copyright holder, the Cleanroom Testing and Certification Board – International, whose course on cleanroom testing the book is based. The author would also like to acknowledge the help of Tim Eaton and Joe Gecsey in the writing of this article. Further information about the book is available from Euromed Communications, at the following web address: https://euromedcommunications.com/collections/books/products/cleanroom-testing-and-monitoring
References
01. Whyte W. Cleanroom Testing and Monitoring 2021. Euromed Communications. ISBN: 978-0-9956666-9-6.
02. Whyte W. Annex A - Monitoring. In ‘Cleanroom Testing and Monitoring’ 2021. Euromed Communications. ISBN: 978-0-9956666-9-6.
03. ISO 14644-1: 2015 Cleanrooms and associated controlled environments - Part 1: Classification of air cleanliness. International Organization for Standardization, Geneva, Switzerland.
04.. Hazard Analysis and Critical Control Point (HACCP), 2017. Available at https://www.food.gov.uk/business-guidance/hazard-analysis-and-critical-control-point-haccp
05. EN IEC 60812: 2018. Failure modes and effects analysis (FMEA and FMECA). CEN - European Committee for Standardization, 1040 Brussels, Belgium.
06. Whyte W. Advances in cleanroom technology 2018. Euromed Communications. ISBN 978-0-9956666-6-5.
07. Eaton T. Pharmaceutical cleanroom classification using ISO 14644-1 and the EU GGMP Annex 1 – Part 1: Testing rationale. European Journal of Parenteral and Pharmaceutical Sciences 2020; 24(4): 1-11. Available at: https://www.ejpps.online/part-1-pharmaceutical-cleanroom-cla
08. Eaton T. Pharmaceutical cleanroom classification using ISO 14644-1 and the EU GGMP Annex 1 – Part 2: Practical application. European Journal of Parenteral and Pharmaceutical Sciences 2020: 24(4): 17-36. Available at: https://www.ejpps.online/pt-2-pharmaceutical-cleanroom-class
09. The rules governing medicinal products in the European Union –Volume 4 EU guidelines to good manufacturing practice - medicinal products for human and veterinary use - Annex 1 -Manufacture of sterile medicinal products 2008. European Commission, Brussels, Belgium.
10. Food and Drug Administration. Guidance for Industry: Sterile Drug Products Produced by Aseptic Processing – Current Good Manufacturing Practice 2004. FDA, Silver Spring, MD, USA.
11. Oakland J and Oakland R. Statistical Process Control – Seventh Edition, 2018. Routledge. ISBN 978-1138064256.
12. ISO 7870 - Control charts. International Organization for Standardization, Geneva, Switzerland.
Author Information
W Whyte
University of Glasgow
Glasgow G12 8QQ
Email: William.Whyte@glasgow.ac.uk




Comments